
Site map










Site map |
||||
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
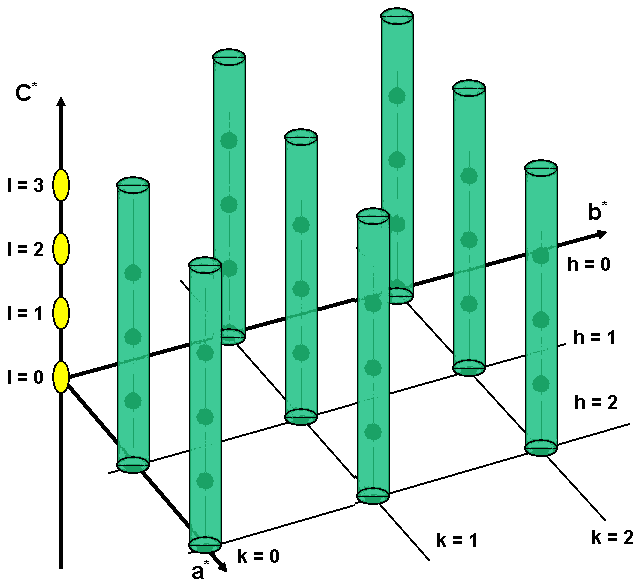
Fig. 1: The reciprocal lattice of a turbostratically disordered layer
structure
From this point of view, the diffraction process can not longer be modelled by Bragg reflections. To calculate the diffraction pattern of such a lattice, it is necessary to integrate in reciprocal space on each spherical surface with 1/d (summary see Brindley, 1980). This method is incompatible with standard Rietveld procedures.
An idea to tackle this problem is the so-called "single layer approach" (Ufer et al., 2004). A single layer (in the case of smectite a 2:1 or TOT layer) is positioned in an c* elongated cell:

Fig. 2: Putting one layer in an elongated cell - the single layer approach
The resulting reciprocal lattice shows series of points that can approximate the rods, but unfortunately this method also creates a meaningless 00l series:
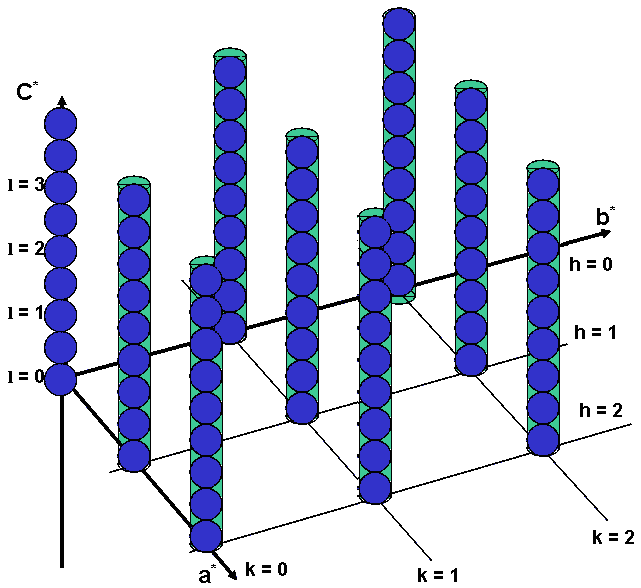
Fig. 3: The reciprocal lattice of a single layer in an elongated cell
However, such redundant lattice points (or reflections) can be sorted out by using the BGMN structure description language. Additionally, separate line broadening parameters for describing the diameter of the rods and the thickness of the stacks can be introduced:
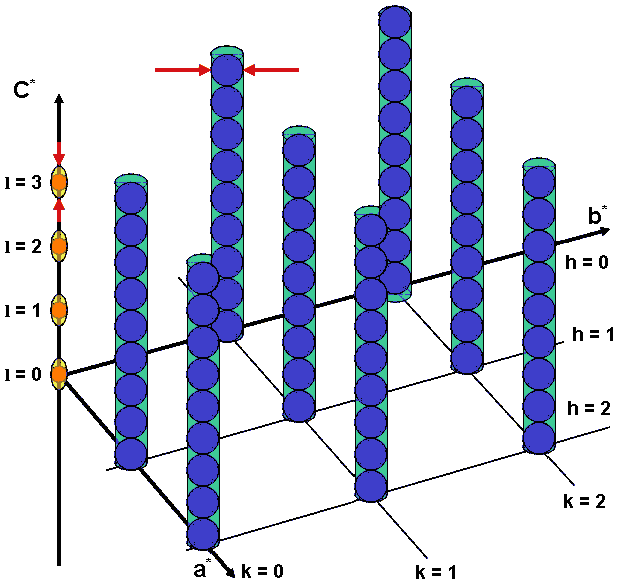
Fig. 4: Schematic sketch of a reciprocal lattice after correcting the
00l series. Broadening parameters are marked by arrows.
Some more formulations of the angular dependency of line broadening are used in order to smooth the calculated pattern between the peak positions (for details, see Ufer et al., 2004).
The example shows a measurement of a natural montmorillonite sample from Budateteny/Hungary. The sample was prepared by wet sieving in distilled water, preserving the natural occupation of the interlayer position. A conventional powder pattern was measured in Bragg-Brentano geometry using an automatic divergence slit, a Co tube and an secondary beam graphite monochromator. The basal spacing of about 1.5 nm at 45 % RH indicates an divalent interlayer cation, mainly Ca as can be assumed from geology.
The structure model was derived from the atomic positions of Tsipursky & Drits (1984) for a cis-vacant 2:1 layer. To avoid a stretching of the structure in c*, the z co-ordinates are formulated to be independent from variations of the c parameter. The interlayer complex is assumed to be an Ca ion, octahedrally surrounded from water molecules represented as oxygen positions. This complex is described as a rigid body, centered in the middle between the 2:1 layers, but allowing turning around the Eulerian angles and shifting in the a-b-plane. Some trials to refine these parameters resulted in a parallel orientation of two faces of the octahedra parallel to the 2:1 layer what is a reasonable result. From this point of view, at least these parameters can be fixed at the resulting values for the analysis of multiphase samples. Other parameters to be refined are the iron content of the octahedra position and the distribution of the octahedral cations on between the trans- and one cis-site. In this case, a cis-vacant occupation was refined. The accuracy or significance of the refinement of the iron content and the occupation of the interlayer site could not be verified until now. These parameters are strongly related to the intensity ratio of the basal reflections. Unfortunately, the correct modelling of the basal series needs a complete homogeneous distribution of water between the layers. This is surely not complete true also for the actual sample. However, the resulting relative low iron occupation of the octahedra (about 10-20 %) appears to be reasonable. The question whether the occupation factors can be refined routineously remains open to further work. All together, the fit of the experimental pattern is quite good:
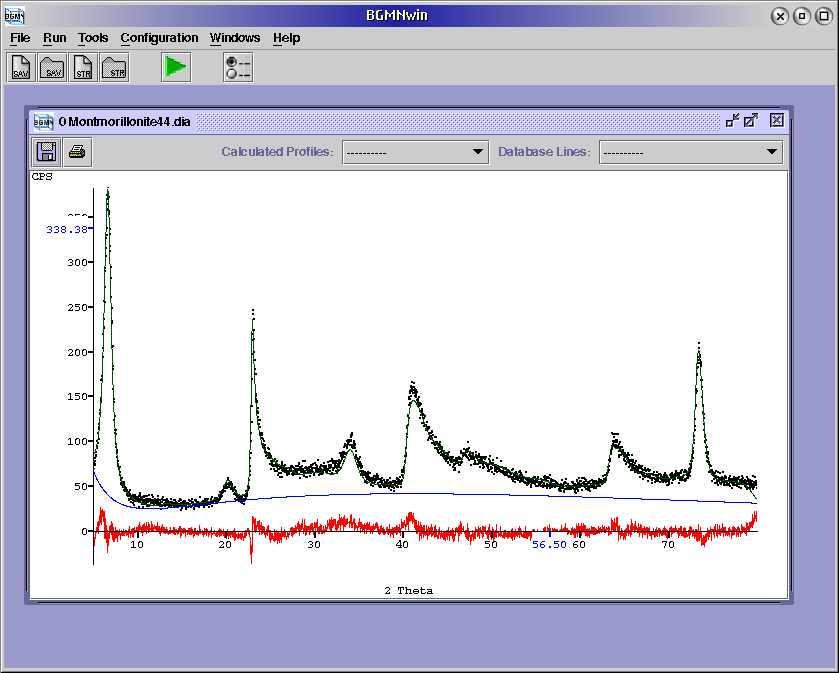
Fig. 5: Rietveld plot of a 15 Å montmorillonite sample. Co radiation,
automatic divergence slit.
The modulation of the 5th order background polynomial with an enhancement around 30°-40° 2Θ could be caused by a very small amount of amorphous material like glass or surface adsorbed water.
An additional trial was done to apply this model to an iron-rich smectite (nontronite). Only the starting values for the lattice parameters have been modified (slightly higher b parameter). The sample (nontronite from Garfield, WA, untreated) was measured in the same geometry as described above, but with a shorter measuring time (5 instead of 20 sec per step). The sample contains some additional goethite. Again, the fitting is remarkable good:
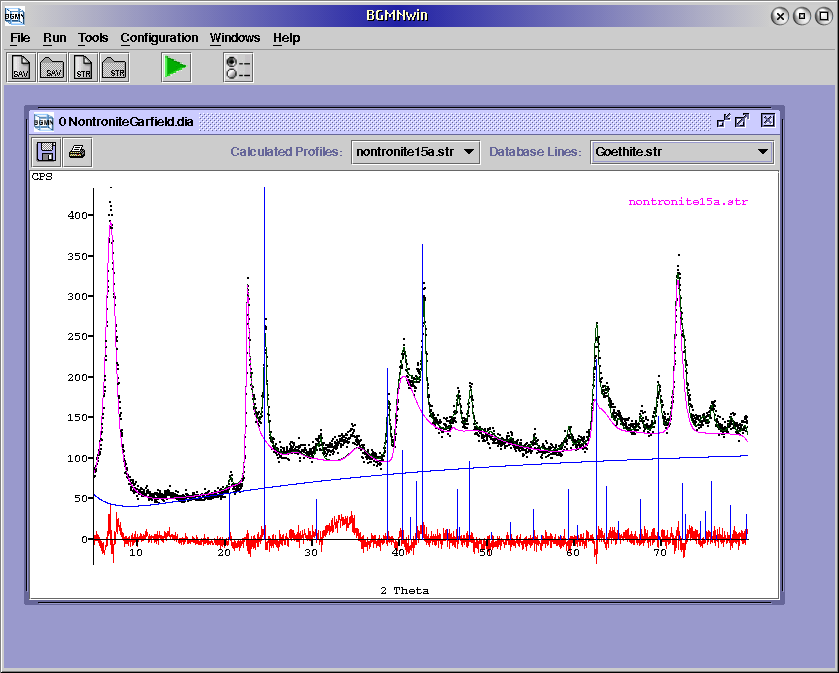
Fig. 6: Rietveld plot of the Garfield nontronite, including the phase profiles.
The misfit around 32°-34° 2Θ could be caused by an non-rational 00l series, indicating some mixed-layering of different hydratation stages. The refinement of the iron content at the octahedral and tetrahedral positions did run at least in the right direction: Very high iron on the octahedra, about 20 % iron on the tetrahedral position. However, further investigations are necessary to check out the potential of this approach for refining of mean structural parameters of smectites.